Teorema de Apolonio

Teorema de Apolonio

En geometría, el teorema de Apolonio, también llamado teorema de la mediana, es un teorema que relaciona la longitud de la mediana de un triángulo con las longitudes de sus lados.

Teorema de Apolonio (teorema de la mediana)

Para todo triángulo la suma de los cuadrados de dos lados cualesquiera, es igual al la mitad del cuadrado del tercer lado más el doble del cuadrado de su mediana correspondiente.

Apolonio de Perga

Para cualquier triángulo ?ABC (véase fig. 1), si M es la mediana correspondiente al lado c, donde AP = PB = ½ c, entonces :

a^2+b^2=\frac{1}{2}\;c^2 + 2\;M^2

 

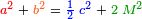Esquema con áreas ? ( {\scriptstyle{ \color{Red} a^2}\;+\;{ \color{Orange} b^2 }\; =\; { \color{Blue} \frac{1}{2}\;c^2 }\;+\;{ \color{OliveGreen} 2\;M^2 }} ).

(227 Posts)

José Aurelio Pina Romero, Licenciado en Ciencias y Técnicas Estadística por la Universidad Miguel Hernández de Elche. Ejerce como profesor de Matemáticas en el IES Bahía de Babel. Es amante de las nuevas tecnologías y metodologías educativas, y en su tiempo libre le gusta practicar deporte y viajar.

Leave a Reply

Your email address will not be published. Required fields are marked *